Answer:
(a) The sample size required is 43.
(b) The sample size required is 62.
Explanation:
The (1 - α) % confidence interval for population mean is:
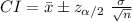
The margin of error for this interval is:
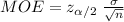
(a)
The information provided is:
σ = 4 minutes
MOE = 72 seconds = 1.2 minutes
Confidence level = 95%
α = 5%
Compute the critical value of z for α = 5% as follows:
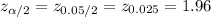
*Use a z-table.
Compute the sample size required as follows:
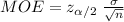
![n=[(z_(\alpha/2)* \sigma)/(MOE) ]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/m2u1k9ijjgct1opmm5ybia07934fgjtdo5.png)
![=[(1.96* 4)/(1.2)]^(2)\\\\=42.684\\\\\approx 43](https://img.qammunity.org/2021/formulas/mathematics/college/pawjj8jpkui0dgvuwdp96ivp99iqky9bgs.png)
Thus, the sample size required is 43.
(b)
The information provided is:
σ = 4 minutes
MOE = 1 minute
Confidence level = 95%
α = 5%
Compute the critical value of z for α = 5% as follows:
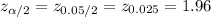
*Use a z-table.
Compute the sample size required as follows:
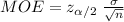
![n=[(z_(\alpha/2)* \sigma)/(MOE) ]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/m2u1k9ijjgct1opmm5ybia07934fgjtdo5.png)
![=[(1.96* 4)/(1)]^(2)\\\\=61.4656\\\\\approx 62](https://img.qammunity.org/2021/formulas/mathematics/college/yqsc8ekfpan6k1v9ug1dki3ucid4fvc5pl.png)
Thus, the sample size required is 62.