Question

A product developer is interested in reducing the drying time of a primer paint. Two formulations of the paint are tested: Formulation-1 is the standard chemistry and formulation-2 is a new drying ingredient that should reduce the drying time. From experience, it is known that the standard deviation drying tine is 8 min and it should not be affected by addition of new ingredient. 10 specimens are painted with each formulation and data is tabulated below:

Parameter Formulation-2 Formulation- 1
Average 121 min 112 min
Sample size 10 10

Required:
a. By hypothesis testing method, check if the addition of new ingredient reduces the drying time. (Write the hypothesis, test statistics, critical region decision). Use alpha = 0.05.
b. What is the P-value of your test?
c. Draw P-value and a value in a standard normal distribution curve.

Answer 1

the answer is in the explanation

Explanation:

we are given

sample size
`n_(1) = n_(2)` = 10 for each formulation

mean
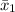`\bar{x} _(1)` (formulation 1) = 121

mean
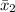`\bar{x} _(2)` (formulation 2) = 112

s (standard deviation ) = 8 mins for each case

null hypothesis
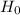`H_(0)` μ2 = μ1 (both have average same time)

alternative hypothesis
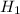`H_(1)` μ2 < μ1

under
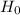`H_(0)` the test statistics is

`t = \frac{\bar{x}_(2) - \bar{x}_(1) }{s\sqrt{(1)/(n_(1) )+ (1)/(n_(1)) } }`

`t = \frac{112 - 121 }{8\sqrt{(1)/(10 )+ (1)/(10) } }`

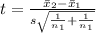
t = -2.5

ItI = 2.5

The P-value at ItI = 2.5 at
`\alpha` = 0.05 μ = 0.010699

check the remaining solution and diagram in the attached image