Question

A girl pushes a 1.04 kg book across a table with a horizontal applied force 10 points

of 15.0 N. If the coefficient of kinetic friction between the book and the
table is 0.35, find its acceleration. *​

Answer 1

Approximately
`11.0\; \rm m \cdot s^(-1)`. (Assuming that
`g = 9.81 \; \rm N \cdot kg^(-1)`, and that the tabletop is level.)

Step-by-step explanation:

Weight of the book:

`W = m \cdot g = 1.04 \; \rm kg * 9.81\; \rm N \cdot kg^(-1) \approx 10.202\; \rm N`.

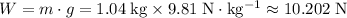If the tabletop is level, the normal force on the book will be equal (in magnitude) to weight of the book. Hence,
`F(\text{normal force}) \approx 10.202\; \rm N`.

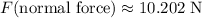As a side note, the
`F_N` and
`W` on this book are not equal- these two forces are equal in size but point in the opposite directions.

When the book is moving, the friction
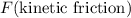`F(\text{kinetic friction})` on it will be equal to

• 
  `\mu_(\rm k)`, the coefficient of kinetic friction, times
• 
  `F(\text{normal force})`, the normal force that's acting on it.

That is:

`\begin{aligned}& F(\text{kinetic friction}) \\ &= \mu_(\rm k)\cdot F(\text{normal force})\\ &\approx 0.35 * 10.202\; \rm N \approx 3.5708\; \rm N\end{aligned}`.

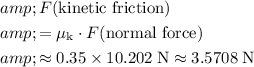Friction acts in the opposite direction of the object's motion. The friction here should act in the opposite direction of that
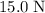`15.0\; \rm N` applied force. The net force on the book shall be:

`\begin{aligned}& F(\text{net force}) \\ &= 15.0 \; \rm N - F(\text{kinetic friction}) \\& \approx 15.0 - 3.5708\; \rm N \approx 11.429\; \rm N\end{aligned}`.

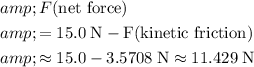Apply Newton's Second Law to find the acceleration of this book:

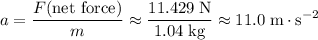`\displaystyle a = \frac{F(\text{net force})}{m} \approx (11.429\; \rm N)/(1.04\; \rm kg) \approx 11.0\; \rm m \cdot s^(-2)`.