Answer:
(a) The test statistic value is -1.83.
(b) We accept the null hypothesis at α = 0.01.
Explanation:
The information provided is:
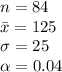
The hypothesis is defined as follows:
H₀: μ ≥ 130 versus Hₐ: μ < 130.
Since the population standard deviation is provided, we will use a z-test.
Compute the test statistic as follows:

The test statistic value is -1.83.
(b)
Compute the p-value of the test as follows:
p-value = P (Z < -1.83)
= 0.034
* Use a z-table.
We reject a hypothesis if the p-value of a statistic is lower than the level of significance α.
• p-value = 0.034 < α = 0.04. Reject the null hypothesis.
• p-value = 0.034 > α = 0.01. Fail to reject the null hypothesis.
• p-value = 0.034 < α = 0.05. Reject the null hypothesis.
• p-value = 0.034 < α = 0.10. Reject the null hypothesis.