Answer:
The radius is
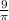 or 2.866
or 2.866
Explanation:
Given
Central angle = 120
Length of arc = 6
Required
The radius
To solve this question, we'll apply the formula of length of an arc.
The length of an arc is calculated as follows;

Where theta = central angle = 120
L = length of the arc = 6.
By substituting these values in the formula above, we have
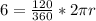

Multiply both sides by 3


Divide both sides by

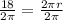
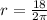
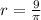
Leaving the answer in terms of
 , the radius is calculated as
, the radius is calculated as
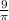
However, if we're to solve further
Taking
 as 3.14
as 3.14
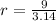
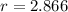
The radius is 2.866