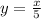Question

Kendra is a blind marathon runner training for the Junior

Paralympics. Kendra's coach graphs a line representing
Kendra's distance from the start over the first 10 minutes of a
practice 5K race. What is the slope of the line? What equation
could you use to find y, Kendra's distance from the start after
x minutes?

Answer 1

Slope =
`(1)/(5)`

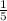
Equation of the line is
`y=(x)/(5)`

Explanation:

Given question is incomplete; find the complete question in the attachment.

Since the given line passes through two points (5, 1) and (10, 2),

Slope of the given line =
`((y_(2)-y_(1)))/((x_(2)-x_(1)))`

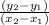
m =
`((2-1))/((10-5))`

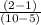
m =
`(1)/(5)`

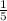
Since the given line passes through (10, 2), equation of the line will be

y - y' = m(x - x')

`y - 2=(1)/(5)(x-10)`

`y=2+(x)/(5)-2`

`y=(x)/(5)`

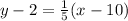
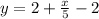
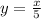
Therefore, equation that can be used to find the distance y from the start after x minutes will be
`y=(x)/(5)`