Answer:
Explanation:
In order to solve this, you must use the distributive property.
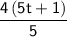
Distributive property:
⇒ A(B+C)=AB+AC
⇒ 4(5t+1)
Multiply by expand.
4*5t=20t
4*1=4
Rewrite the problem down.
20t+4
20t+4/5
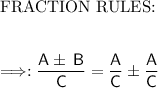
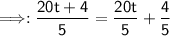
You have to divide the numbers from left to right.
⇒ 20/5=4
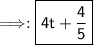
- Therefore, the correct answer is 4t+4/5.