Question

A researcher with the Ministry of Transportation is commissioned to study the drive times to work (one-way) for U.S. cities. The underlying hypothesis is that average commute times are different across cities. To test the hypothesis, the researcher randomly selects six people from each of the four cities and records their one-way commute times to work. Refer to the below data on one-way commute time (in minutes) to work. Note that the grand mean is 36.625.

Houston Charlotte Tucson Akron
45 25 25 Id
65 30 30 15
105 35 19 15
55 10 30 10
85 50 10 5
90 70 35 10
bar{x}_i 74.167 36.667 24.833 10.833
s_i^2 524.167 436.667 82.167 14.167
At the 5% significance level, the critical value is:
a. 4.94.
b. 3.10.
c. 3.86.
d. 2.38

Answer 1

Check the explanation

Explanation:

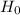`H_(0)`: all means are equal (i.e. null hypothesis)

Ha: at least one mean is different (i.e. alternative hypothesis)

Mean n Std. Dev

74.2 6 22.89 Houston

36.7 6 20.90 Charlotte

24.8 6 9.06 Tucson

10.8 6 3.76 Akron

36.6 24 28.41 Total

ANOVA table

Source SS df MS F p-value

Treatment 13,281.79 3 4,427.264 16.75 1.11E-05

Error 5,285.83 20 264.292

Total 18,567.63 23

The test statistic is

F=16.75

Given a=0.05, the critical value is F(0.95, df1=3, df2=20) =3.10 (from F table)

Since F=16.75 is larger than 3.10, we reject
`H_0`.

So we can conclude that average commute times are different across cities