Question

A random sample of 16 airline passengers at the Monroe airport showed that the mean time spent waiting in line to check in at the ticket counters was 31 minutes, with standard deviation of 7 minutes. Construct a 99% confidence interval for the mean wait time by all passengers at the Monroe airport, assuming the wait times for all passengers are normally distributed. The following information was obtained from two independent samples selected from two populations with unknown but equal standard deviations.

n_1 = 55 x- = 90.40 S_1 = 11.60
n_2 = 55 x-2 = 86.30 s_2 = 10.25
1. What is the point estimate of mu_1 - mu_2?
2. Construct a 99% confidence interval for mu_1 - mu_2.

Answer 1

(a) 99% confidence interval for the mean wait time by all passengers at the Monroe airport is [25.84 hours , 36.16 hours].

(b) 99% confidence interval for the difference between population means (
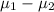`\mu_1-\mu_2`) is [-1.38 , 9.58].

Explanation:

(a) We are given that a random sample of 16 airline passengers at the Monroe airport showed that the mean time spent waiting in line to check in at the ticket counters was 31 minutes, with standard deviation of 7 minutes.

Firstly, the Pivotal quantity for 99% confidence interval for the population mean wait time is given by;

P.Q. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean time spent waiting in line = 31 minutes

s = sample standard deviation = 7 minutes

n = sample of airline passengers = 16

`\mu` = population mean wait time by all passengers

Here for constructing 99% confidence interval we have used One-sample t test statistics as we don't know about population standard deviation.

So, 99% confidence interval for the population mean,
`\mu` is ;

P(-2.947 <
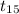`t_1_5` < 2.947) = 0.99 {As the critical value of t at 15 degree

of freedom are -2.947 & 2.947 with P = 0.5%}

P(-2.947 <
`(\bar X-\mu)/((s)/(√(n) ) )` < 2.947) = 0.99

P(
`-2.947 * {(s)/(√(n) ) }` <
`{\bar X-\mu}` <
`2.947 * {(s)/(√(n) ) }` ) = 0.99

P(
`\bar X-2.947 * {(s)/(√(n) ) }` <
`\mu` <
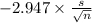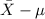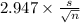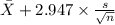`\bar X+2.947 * {(s)/(√(n) ) }` ) = 0.99

99% confidence interval for
`\mu` = [
`\bar X-2.947 * {(s)/(√(n) ) }` ,
`\bar X+2.947 * {(s)/(√(n) ) }` ]

= [
`31-2.947 * {(7)/(√(16) ) }` ,
`31+2.947 * {(7)/(√(16) ) }` ]

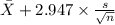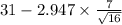= [25.84 , 36.16]

Therefore, 99% confidence interval for the mean wait time by all passengers at the Monroe airport is [25.84 hours , 36.16 hours].

(b) Now, we are given the following information that was obtained from two independent samples selected from two populations with unknown but equal standard deviations.

n_1 = 55 x-1 = 90.40 s_1 = 11.60

n_2 = 55 x-2 = 86.30 s_2 = 10.25

Firstly, the Pivotal quantity for 99% confidence interval for the difference between population means is given by;

P.Q. =
`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` ~
`t__n__1-_n__2-2`

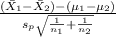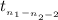
where,
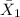`\bar X_1` = sample mean of first sample = 90.40

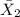`\bar X_2` = sample mean of second sample = 86.30

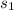`s_1` = sample standard deviation of first sample = 11.60

`s_2` = sample standard deviation of second sample = 10.25

`n_1` = size of first sample = 55

`n_2` = size of second sample = 55

Also,
`s_p=\sqrt{((n_1-1)s_1^(2) +(n_2-1)s_2^(2) )/(n_1+n_2-2) }` =
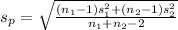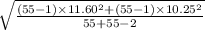`\sqrt{((55-1)* 11.60^(2) +(55-1)* 10.25^(2) )/(55+55-2) }` = 10.95

Here for constructing 99% confidence interval we have used Two-sample t test statistics as we don't know about population standard deviations.

So, 99% confidence interval for the difference between population means, (
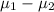`\mu_1-\mu_2`) is ;

P(-2.626 <
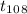`t_1_0_8` < 2.626) = 0.99 {As the critical value of t at 108 degree

of freedom are -2.626 & 2.626 with P = 0.5%}

P(-2.626 <
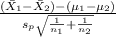`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` < 2.626) = 0.99

P(
`-2.626 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` <
`{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}` <
`2.626 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` ) = 0.99

P(
`(\bar X_1-\bar X_2)-2.626 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` < (
`\mu_1-\mu_2`) <
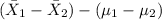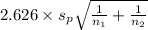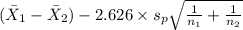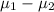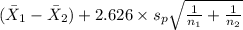`(\bar X_1-\bar X_2)+2.626 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` ) = 0.99

99% confidence interval for (
`\mu_1-\mu_2`) =

[
`(\bar X_1-\bar X_2)-2.626 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` ,
`(\bar X_1-\bar X_2)+2.626 * {s_p\sqrt{(1)/(n_1) +(1)/(n_2) } }` ]

= [
`(90.40-86.30)-2.626 * {10.95 * \sqrt{(1)/(55) +(1)/(55) } }` ,
`(90.40-86.30)+2.626 * {10.95 * \sqrt{(1)/(55) +(1)/(55) } }` ]

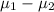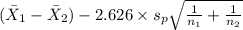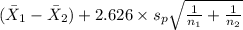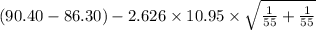= [-1.38 , 9.58]

Therefore, 99% confidence interval for the difference between population means (
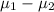`\mu_1-\mu_2`) is [-1.38 , 9.58].