Answer:
No. There is not enough evidence to support the claim that the population standard deviation is different from $12.
Explanation:
The null hypothesis is that the true standard deviation is 12.
The alternative hypothesis is that the true standard deviation differs from 12.
We can state:
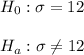
The significance level is 0.10.
The sample size is n=15, so the degrees of freedom are:

The sample standard deviation is 9.25.
The test statistic is
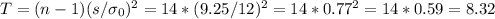
The critical values for rejecting the null hypothesis are:
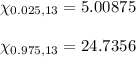
As T=8.32 is within the acceptance region (5.01, 24.74), the null hypothesis failed to be rejected.
There is not enough evidence to support the claim that the population standard deviation is different from $12.