Question

You work for a cereal company as a box designer. Your job is to find the dimensions of a box. The volume of the box is given by the following:

v(x)=8x^3-108x^2+360


a. Use a graphing calculator to determine the length, width, and height of the box so it will hold the largest possible volume.


b. Factor the polynomial completely to find the x-intercepts of the graph. In context of this problem, what do the intercepts represent?


c. What is the domain and range for the box?

Answer 1

Question:

You work for a cereal company as a box designer. Your job is to find the dimensions of a box. The volume of the box is given by the following:

v(x)=8·x³-108·x²+360·x

Answer:

a. To hold the largest possible volume, the length, height, and width are;

Length, l of the box = 10.583

Width, w of the box = 3.791

Height, h of the box = 8.835

b. The x intercepts are;

x = 0

x = 15/2

x = 6

The intercept represents the points of the function at which the volume of the box change from negative to negative and back to positive

c. The domain range is all real numbers, that is from -∞ to +∞

Explanation:

Since the volume V(x) = 8·x³ - 108·x² + 360·x, we have fo maximum volume;

`\frac{\mathrm{d} \left (8\cdot x^(3) - 108\cdot x^(2) + 360\cdot x \right )}{\mathrm{d} x}= 0`

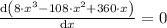
Therefore. 24·x² - 216·x + 360 = 0

Solving the quadratic equation, we have

(2·x - (9 - √21))(2·x - (9 + √21))

Therefore, x = (9 - √21)/2 or x = (9 + √21)/2

P

Therefore, from the v(x) equation we have by factorizing;

v(x) = 8·x³ - 108·x² + 360·x = 4·x·(2·x - 15)·(x - 6)

Plugging the possible values of x for maximum v(x), we obtain

For x = (9 - √21)/2, v(x) = 354.468

For x = (9 + √21)/2, v(x) = -30.468

Hence the for maximum v(x), x = (9 - √21)/2

The sides are thus;

4·x·(2·x - 15)·(x - 6)

Where:

4·x = 8.835

`\left |2\cdot x - 15 \right |` = 10.583

`\left | x - 6\right |` = 3.791

The length, l of the box = 10.583

The width, w of the box = 3.791

The height, h of the box = 8.835

b. The factorization of the polynomial gives;

v(x) = 4·x·(2·x - 15)·(x - 6)

Therefore, the x intercepts are;

x = 0

x = 15/2

x = 6

The intercept represents the points of the function at which the volume of the box will be positive, hence the possible values of the dimensions

c. The domain of the function v(x) = 8·x³ - 108·x² + 360·x (which is a polynomial without variables or radicals as the denominator) is the set of all real numbers from -∞ to ∞.