Question

Which of the following measurements could be the side lengths of a right triangle? A 60 in, 96 in, 120 in B 72 in, 108 in, 120 in C 72 in, 96 in 120 in D 72 in, 96 in, 144 in

Answer 1

Option C could be the side lengths of a right triangle

Explanation:

A) 60 in, 96 in, 120 in

Longest side = hypotenuse = 120 inch

To check measurements could be the side lengths of a right triangle

We will use Pythagoras theorem :

`Hypotenuse^2=Perpendicular^2+Base^2\\120^2=60^2+96^2\\14400 \\eq 12816`

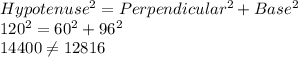
So, It is not a right angled triangle

B)72 in, 108 in, 120 in

Longest side = hypotenuse = 120 inch

To check measurements could be the side lengths of a right triangle

We will use Pythagoras theorem :

`Hypotenuse^2=Perpendicular^2+Base^2\\120^2=72^2+108^2\\14400 \\eq 16848`

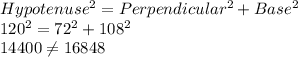
So, It is not a right angled triangle

C)72 in, 96 in 120

Longest side = hypotenuse = 120 inch

To check measurements could be the side lengths of a right triangle

We will use Pythagoras theorem :

`Hypotenuse^2=Perpendicular^2+Base^2\\120^2=72^2+96^2\\14400 =14400`

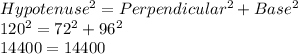
So, It is a right angled triangle

D) 72 in, 96 in, 144 in

Longest side = hypotenuse = 144 inch

To check measurements could be the side lengths of a right triangle

We will use Pythagoras theorem :

`Hypotenuse^2=Perpendicular^2+Base^2\\144^2=72^2+96^2\\20736 \\eq 14400`

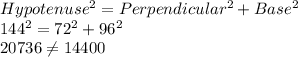
So, It is a not right angled triangle

So, Option C could be the side lengths of a right triangle