Graph a parabola whose x-intercepts are at x=-3 and x=5 and whose minimum value is y=-4

Question

asked Mar 26, 2021 193k views

1 Answer

Gamma · Answer 1 · 2021-03-31T12:49:08+0000

Answer:

(See explanation for further details)

Explanation:

The standard equation of the parabola is:

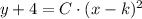
$y + 4 = C \cdot (x-k)^(2)$

The formula is now expanded into a the form of a second-order polynomial:

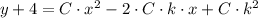
$y + 4 = C\cdot x^(2) -2\cdot C\cdot k \cdot x +C\cdot k^(2)$

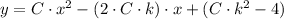
$y = C\cdot x^(2) - (2\cdot C \cdot k) \cdot x + (C\cdot k^(2)-4)$

The general equation of the second-order polynomial is:

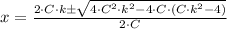
$x = \frac{2\cdot C \cdot k \pm \sqrt{4\cdot C^(2)\cdot k^(2)-4\cdot C\cdot (C\cdot k^(2)-4)}}{2\cdot C}$

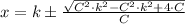
$x = k \pm \frac{\sqrt{C^(2)\cdot k^(2)-C^(2)\cdot k^(2)+4\cdot C}}{C}$

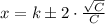
$x = k \pm 2\cdot (√(C))/(C)$

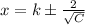
$x = k \pm (2)/(√(C))$

The equations to be solved are presented herein:

-3 = k -(2)/(√(C))

5 = k + (2)/(√(C))

Now, the solution of the system is:

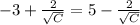
-3 +(2)/(√(C)) = 5 -(2)/(√(C))

(4)/(√(C)) = 8

√(C) = (1)/(2)

C = (1)/(4)

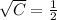
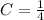
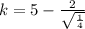
$k = 5 - \frac{2}{\sqrt{(1)/(4) }}$

k = 1

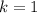
The equation of the parabola is:

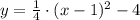
$y = (1)/(4)\cdot (x-1)^(2) -4$

Lastly, the graphic of the function is included as attachment.