Question

The distribution of math SAT scores is normally distributed with a mean of 500 and a standard deviation of 90.

a) Find the percentage of people scoring above a 700.
b)Find the percentage of people who score between 450 and 550
c)Find the z score of a person who scores 680
d)Find the probability of having a z score less than -1.42
e)You score a 710 on your math SAT. Is this score unusual? Explain.

Answer 1

a) 1.39%

b) 42.26%

c) 97.72%

d) 7.78%

e) 99.01%

Explanation:

mean (μ) = 500, standard deviation (σ) = 90

The z score is used to measure the amount by which the raw score is above or below the mean. It is given by:

`z=(x-\mu)/(\sigma)`

a) For x > 700

`z=(x-\mu)/(\sigma)=(700-500)/(90) =2.22`

From the probability distribution table:

P(x > 700) = P(z > 2.22) = 1 - P(z < 2.22) = 1 -0.9861 = 0.0139 = 1.39%

b) For x = 450

`z=(x-\mu)/(\sigma)=(450-500)/(90) =-0.56`

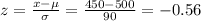
For x = 550

`z=(x-\mu)/(\sigma)=(550-500)/(90) =0.56`

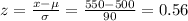
From the probability distribution table:

P(450< x < 550) = P(z < 0.56) - P(z < -0.56) = 0.7123 - 0.2877 = 0.4246 = 42.46%

c) For x < 680

`z=(x-\mu)/(\sigma)=(680-500)/(90) =2`

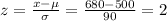
From the probability distribution table:

P(x < 680) = P(z < 2) = 0.9772 = 97.72%

d) From the probability distribution table: P(z < -1.42) = 0.0778 = 7.78%

e) c) For x = 710

`z=(x-\mu)/(\sigma)=(710-500)/(90) =2.33`

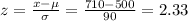
From the probability distribution table: P(x < 710) = P(z < 2.33) = 0.9901 = 99.01%