Question

Rao's Finance claims that less than 50% of adults in Suva have a will. A will is a legal

document that sets forth your wishes regarding the distribution of your property and the care of
any minor children. If you die without a will, those wishes may not be carried out. To
substantiate the claim, a random sample of 1000 adults showed that 450 of them have a willwill

A At the 5% significance level, can you conclude that the percentage of people who have a
will is less than 50%?

B. What is the Type I error in part A? What is the probability of making this error?

C. What would your decision be in part A if the probability of making a Type I error were
zero? Explain​

Answer 1

Explanation:

Given:

Sample size, n= 1000

`X = (450)/(1000) = 0.45`

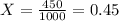
P' = 0.5

Level of significance, a = 0.05

a) The null and alternative hypotheses:

H0 : u ≥ 0.5

H1 : u < 0.5

This is a left tailed test.

Decision:

Reject null hypothesis H0 if p value is less than level of significance.

The test statistic, z =

`(0.45 - 0.5)/(0.5/ √(1000))`

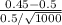
z = - 3.1623

From the standard normal table,

NORMSDIST(-3.1623)= 0.00078 ≈ 0.0008

Pvalue = 0.0008

Since p value, 0.0008 is less than significance level 0.05, we reject H0.

In conclusion, there is sufficient evidence to evidence to reject H0.

b) The type I error here is the claim that less than 50% of adults have a will, whereas the probability is not less than 50%.

Probability of type I error = significance level = 0.05

c)What would your decision be in part A if the probability of making a Type I error were zero?

If probability of making a type I error were zero in part A, we are to reject the null hypothesis, H0.