Question

Triangle ABC is a right triangle. Sides AB and BC form the right angle. The equation of the line representing side AB is 3x+ 6y = 12. if C is located at

the point (9,5), what is the equation of the line representing side BC ?

Answer 1

We have been given that triangle ABC is a right triangle. Sides AB and BC form the right angle. The equation of the line representing side AB is
`3x+ 6y = 12`.

We are asked to find the equation of the line representing side BC, if C is located at the point (9,5).

Since sides AB and BC form the right angle, so AB and BC are perpendicular each other.

We know that slopes of perpendicular lines are negative reciprocal of each other.

First of all, we will convert equation of line AB into slope-intercept form as:

`3x-3x+ 6y = 12-3x`

`6y=-3x+12`

`(6y)/(6)=-(3)/(6)x+(12)/(6)`

`y=-(1)/(2)x+2`

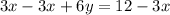
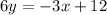
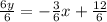
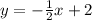
We can see that slope of line AB is
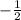`-(1)/(2)`. Slope of line BC will be negative reciprocal of
`-(1)/(2)`.

`-(-(1)/((1)/(2)))=-(-2)=2`

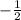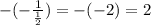
Now we will use point (9,5) to write the equation as:

`y-y_1=m(x-x_1)`

`y-5=2(x-9)`

`y-5=2x-18`

`y-5+5=2x-18+5`

`y=2x-13`

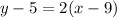
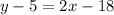
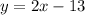
Therefore, the equation of the line BC would be
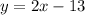`y=2x-13`.