Question

The average age of a breed of dog is 19.4 years. If the distribution of their ages is normal and

20% of dogs are older than 22.8 years, find the standard deviation.
​

Answer 1

We have been given that the average age of a breed of dog is 19.4 years. The distribution of their ages is normal and 20% of dogs are older than 22.8 years. We are asked to find the standard deviation.

Since 20% of dogs are older than 22.8 years, so 80% of dogs are younger than 22.8.

We will use z-score formula to solve our given problem.

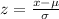`z=\frac{x-\mu}\sigma}`, where,

z = z-score,

x = Random sample score,

`\mu` = Mean,

`\sigma` = Standard deviation.

Now we will use normal distribution table to find the z-score corresponding to 80% or
`0.80`.

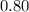z-score corresponding to 0.80 is 0.845.

Upon substituting our given values in z-score formula, we will get:

`0.845=(22.8-19.4)/(\sigma)`

`\sigma=(22.8-19.4)/(0.845)`

`\sigma=(3.4)/(0.845)`

`\sigma=4.0236`

`\sigma\approx 4.02`

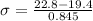
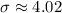
Therefore, the standard deviation is approximately 4.02 years.