Answer:
a)
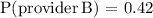
b)
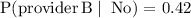
Explanation:
The joint probability table is attached below.
There are three different wireless telecommunication providers.
1. Provider A
2. Provider B
3. Provider C
The survey asks the customers whether they have cell phone service at the restaurant.
The 'Yes' and 'No' probabilities refer to the cell phone service.
a) Find the probability that a randomly selected customer has a contract with provider B.
The required probability is given by

b) Find the probability that a randomly selected customer who does not have cell phone service has a contract with provider B.
The required probability is given by

Moreover, the two events having a contract with provider B and not having cell phone service are independent events since P(provider B) is equal to the P(provider B | No)