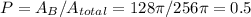Answer:
50%
Explanation:
The end goal here is to find the total area of the entire figure from the center to the outer radius D. Then take the ratio of region B with respect to the total area, which will give you the probability of landing in the area B.
Circle A has a radius of 4. Circle B has a radius of 8. Circle C has a radius of 12. Circle D has a radius of 16. Therefore, the total area of the dartboard is given by:

The area of the region B can be found by thinking of region B as a shaded region between two concentric circles A and C. The area of the circle C is given by:
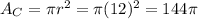
The area of circle A is given by:
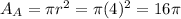
Therefore the area of region B would be:
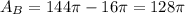
Finally, the probability of landing in region B would be: