Question

A national poll by the Institute for College Access and Success showed that in 69% of college graduates from public and nonprofit colleges in 2013 had student loan debt. Dr. Blackman wanted to find out if her public nonprofit university had a lower proportion of students who graduated with student loan debt in 2013. For this survey, the null hypothesis was that the proportion of students with graduated with student loan debt equals 69% and the alternative hypothesis is that the proportion with student loan debt does not equal 69%. The significance level for this test was 0.05. The results of the hypothesis test of the new survey showed a p-value of 0.039. Which of the following statements is correct?

A. The results were statistically significant.
B. The results were not statistically significant.
C. The null hypothesis should be rejected.
D. The null hypothesis should be accepted.
E. The null hypothesis cannot be rejected.

Answer 1

A. The results were statistically significant.

C. The null hypothesis should be rejected.

Explanation:

We are given that a national poll by the Institute for College Access and Success showed that in 69% of college graduates from public and nonprofit colleges in 2013 had student loan debt.

Let p = proportion with student loan debt.

So, Null Hypothesis,
`H_0` : p = 69% {means that the proportion of students with graduated with student loan debt equals 69%}

Alternate Hypothesis,
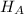`H_A` : p
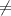`\\eq` 69% {means that the proportion with student loan debt does not equal 69%}

The test statistics that would have used here was One-sample z proportion statistics;

We are given the level of significance of 0.05 and P-value of 0.039.

Since, P-value of the test statistics is less than the level of significance as 0.039 < 0.05, so we have sufficient evidence that the results were statistically significant to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the proportion with student loan debt does not equal 69%.