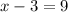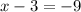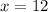Answer:
x = 12 and x = -6
Explanation:
First subtract 6x on both sides to get a 2nd degree polynomial equal to zero:

To complete the square, the formula is to divide 'b' by 2 and square the result. The general form for a 2nd degree polynomial of the variable 'x' is as follows:

For your case, b = 6. Therefore, the term that must be added and subtracted to our equation is:
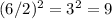
Add and subtract 9 to our equation to get:
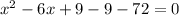
The first three terms form a perfect square, we have:
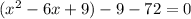
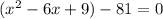
What multiplies to equal 9 but adds to equal -6? That would be -3 and -3. Therefore:
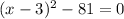
Add 81 to both sides to get:
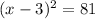
We want to take the square root, but recall a square root has a positive and negative branch. Therefore we have two solutions: