Answer:
True
True
False
Explanation:
TRUE
If the equation Ax = 0 has only the trivial solution, then A is row equivalent to the n × n identity matrix
Here's why
If the equation Ax = 0 has only the trivial solution the determinant of the matrix is NOT 0 and the matrix is invertible therefore it is row equivalent to the nxn identity matrix.
TRUE
If the columns of A span ℝ^n , then the columns are linearly independent
Here's why
Remember that the rank nullity theorem states that
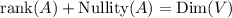
According to the information given we know that
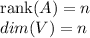
Therefore you have
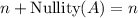
and
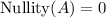
Which is equivalent to the problem we just solved.
FALSE
If A is an n × n matrix, then the equation Ax = b has at least one solution for each b in ℝ^n
Here's why
Take b as a non null vector and A=0, then Ax = 0 and Ax=b will have no solution.