Question

Find the perimeter of quadrilateral ABCD. Round to the nearest tenth.

Answer 1

Perimeter = 13.5 units

Explanation:

Coordinates of A → (1, 2)

Coordinates of B → (2, 5)

Coordinates of C → (5, 7)

Coordinates of D → (4, 4)

Length of AB =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1)})^2}`

=
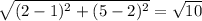`√((2-1)^2+(5-2)^2)=√(10)` units

Length of BC =
`√((5-2)^2+(7-5)^2)`

=
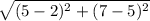
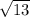`√(13)` units

Length of CD =
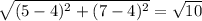`√((5-4)^2+(7-4)^2)=√(10)` units

Length of AC =
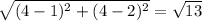`√((4-1)^2+(4-2)^2)=√(13)` units

Perimeter of the quadrilateral =
`2(√(10)+√(13))`

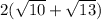
= 2(3.16 + 3.61)

= 13.54

≈ 13.5 units

Perimeter of the quadrilateral ABCD is 13.5 units