Question

A flat disk of material has the same mass as the Earth, 5.98E24 kg, and has a radius of 6.25E07 m. Point A is located a distance of 7.83E06 m above the center of the disk. Point B is located right at the center of the disk. Treat all of the mass as if it were located in the x-y plane. An object of mass 250 kg is located near the disk.

a. Find the gravitational potential energy (J) when the object is at point A.

b. Find the gravitational potential energy (J) when the object is at point B.

c. Find the kinetic energy (J) of an object that has fallen to point B from rest at point A.

Hint: To calculate the potential, break the disk up into a bunch of small pieces and add up the potential due to all of them (i.e. integrate over them - see the section on Center of Mass to get an idea of how to do this. It isnt exactly the same, but similar methods are used.) Dont round your numbers before you calculate part c. Your answer to part c should have two significant figures.

Looking for a solid answer no BS answers please!

Answer 1

Step-by-step explanation:

a. To find the gravitational potential energy you take into account the potential energy generated by a piece of mass in the disk. You also take into account that the gravitational field at point A points to the center of the disk. Then, you can consider an element of the force, Fx:

`F_x=\int G(mdM)/(R^2+a^2)=\int G(m\rho r dr d\theta )/(R^2+a^2)`

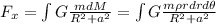
m: mass of a body at a distance of "a" perpendicular to the disk.

R:radius of the disk

M: mass of the disk

G: Cavendish's constant

by solving the integral you obtain:

`F_x=2(GmM)/(R^2)[1-cos\theta]`

`F_x=2GmM[1-(a)/(√(R^2+a^2))]` (1)

To find the gravitational energy you use:

`U=-\int F_x dx=-\int[2GmM(1-(x)/(√(R^2+x^2)))]dx\\\\U=-2GmM[x+√(R^2+x^2)]\\\\U=-2GmM[a+√(R^2+a^2)]`

you replace the values of the parameters in the point A:

`U=-2(6.67*10^(-11))(250)(5.98*10^(24))[(7.83*10^6)+(√((7.83*10^6)^2+(6.25*10^7)^2))]\\\\U=-1.41*10^(25)J`

b. For point B you have a=0.

`U=-2(6.67*10^(-11))(250)(5.98*10^(24))[(7.83*10^6)+(√(((7.83*10^6)^2))]\\\\U=-3.12*10^(24)J`

c. To find the kinetic energy you use:

`W_n=\Delta K\\\\F_xd=(1)/(2)m(v_f^2-v_o^2)`

However, the net work is also the difference between the gravitaional potential energies calculated in the previous steps.