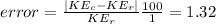Question

Suppose a spacecraft of mass 17000 kg is accelerated to 0.14c. How much kinetic energy would it have? If you used the classical formula for kinetic energy, by what percentage would you be in error?

Answer 1

1.32% error

Step-by-step explanation:

You can derive the relativistic kinetic energy by integrating the velocity function over a differential change in momentum. Then use integration by parts to get the answer of:

`KE=mc^2[gamma-1]`

Gamma is the lorentz factor equal to:

`gamma=(1)/(√(1-(v/c)^2))`

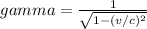
Therefore the relativistic kinetic energy would be:

`KE=mc^2[(1)/(√(1-(v/c)^2))-1]`

Plug everything in to get:

`KE=(17000)(3x10^8)^2[(1)/(√(1-(0.14c/c)^2))-1]`

`KE=(17000)(9x10^(16))[(1)/(√(1-0.0196))-1]`

`KE=1.53x10^(21)[(1)/(√(1-0.0196))-1]`

`KE=1.52x10^(19)J`

The classical non-relativistic formula for kinetic energy is:

`KE=(1)/(2) mv^2`

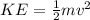
Therefore the classical kinetic energy is:

`KE=1.50x10^(19)J`

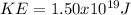
Use the error percentage formula, found online if you dont recall:

`error=(|KE_c-KE_r|)/(KE_r) (100)/(1) =1.32`