Question

A professor believes the class he is teaching in the current semester is above the average of the classes he has taught. In order to test this hypothesis, he analyses the scores of midterm of all 120 students he teaches this semester.Their average score of this exam is 82 out of 100, with a standard deviation of 12. The mean score of the midterm for all students that he has taught for the last thirty-two years is 78 out of 100, with a standard deviation of 15. Use an alpha level of 0.01 for this analysis.

1) z test or t test?
2) calculate the obtained statistic
3) make a decision
4) what does your decision mean

Answer 1

1) Since we know the info from all the students that he teaches and we know the population deviation from past data we can use a z test to check the hypothesis

2)
`t=(82-78)/((15)/(√(120)))=2.921`

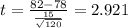
3)
`p_v =P(Z>2.921)=0.0017`

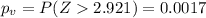
Since the p value is lower than the significance level of 0.01 we have enough evidence to reject the null hypothesis in favor of the alternative hypothesis

4) For this case since we reject the null hypothesis we have enough evidence ot conclude that the scores for this semester are above the historical value of 78 so then the claim stated by the teacher makes sense

Explanation:

Part 1

Since we know the info from all the students that he teaches and we know the population deviation from past data we can use a z test to check the hypothesis

Part 2

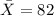`\bar X=82` represent the sample mean for the scores

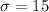`\sigma=15` represent the population standard deviation

n=120 represent the sample selected

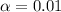`\alpha=0.01` significance level

System of hypothesis

He wants to test if the group for this current semester is above the average of the classes he has taught (mean 78), the system of hypothesis are:

Null hypothesis:
`\mu \leq 78`

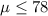
Alternative hypothesis:
`\mu > 78`

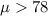
Since we know the population deviation we can use the following statistic

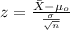`z=(\bar X-\mu_o)/((\sigma)/(√(n)))` (1)

Replacing the info given we got:

`t=(82-78)/((15)/(√(120)))=2.921`

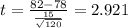
Part 3

We can calculate the p value for this test with this probability taking in count the alternative hypothesis:

`p_v =P(Z>2.921)=0.0017`

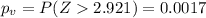
Since the p value is lower than the significance level of 0.01 we have enough evidence to reject the null hypothesis in favor of the alternative hypothesis

Part 4

For this case since we reject the null hypothesis we have enough evidence ot conclude that the scores for this semester are above the historical value of 78 so then the claim stated by the teacher makes sense