Answer:
Probability that the average pulse of the 100 adults is between 78 and 81 beats per minute is 0.7493.
Explanation:
We are given that adult between the age of 21 and 65 have a mean pulse of 80 beats per minute with a standard deviation of 12 beats per minute.
A doctor measures 100 random, independent adults between the ages of 21 and 65 from the population of such adults and calculates their average pulse.
Let
 = sample average pulse
= sample average pulse
The z score probability distribution for sample mean is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean pulse = 80 beats per minute
= population mean pulse = 80 beats per minute
 = standard deviation = 12 beats per minute
= standard deviation = 12 beats per minute
n = sample of adults measured = 100
Now, probability that the average pulse of the 100 adults is between 78 and 81 beats per minute is given by = P(78 <
 < 81)
< 81)
P(78 <
 < 81) = P(
< 81) = P(
 < 81) - P(
< 81) - P(

 78)
78)
P(
 < 81) = P(
< 81) = P(
 <
<
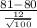 ) = P(Z < 0.83) = 0.79673
) = P(Z < 0.83) = 0.79673
P(

 78) = P(
78) = P(


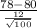 ) = P(Z
) = P(Z
 -1.67) = 1 - P(Z < 1.67)
-1.67) = 1 - P(Z < 1.67)
= 1 - 0.95254 = 0.04746
Therefore, P(78 <
 < 81) = 0.79673 - 0.04746 = 0.7493
< 81) = 0.79673 - 0.04746 = 0.7493