Question

Find all zeros of ƒ(x) = 2x^4 – 72x^2. Then determine the multiplicity at each zero. State whether the graph will touch or cross the x-axis at the zero.

Answer 1

Answer: See below

Explanation:

To find the factor,

f(x) = 0

`\begin{aligned}&2 x^(4)-72 x^(2)=0 \\&2 x^(2)\left(x^(2)-36\right)=0 \\&x^(2)\left(x^(2)-36\right)=0 \\&x * x *(x-6) *(x+6)=0 \\&\mathrm{x}=0,0,6,-6\end{aligned}`

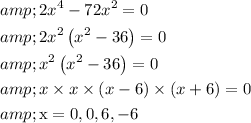
So,

x = 0 multiplicity 2

x = -6 multiplicity 1

x = 6 multiplicity 1

For an even multiplicty, the graph touches the x-axis, and for an odd multiplicty, the graph crosses the x-axis

Therefore,

x = 0 multiplicty 2, Touch

x = -6 multiplicty 1, Cross

x = 6 multiplicty 1, Cross