Question

Jefferson is plotting the vertices of an isosceles right triangle on a coordinate graph. He has

plotted the two points shown. Where should he plot the third point?
I (-2,0)
(-2,-9)
(3,1)
(4,2)

Answer 1

Option (4).

Explanation:

Given question is incomplete; here is the complete question.

Jefferson is plotting the vertices of an isosceles right triangle on a coordinate graph. He has plotted the two points shown. Where should he plot the third point?

The point is on the graph is (-2,-4) (4,-4)

The options are

(-2,-9)

(3,1)

(-2,0)

(4,2)

Distance between (-2, -4) and (4, -4) = 6 units

Now we will check every option,

1). For point (-2, -9),

Distance between (-2, -4) and (-2, -9) =
`√((-2+2)^2+(-4+9)^2)=5`

Similarly, distance between (4, -4) and (-2, -9) =
`√((4+2)^2+(-4+9)^2)=√(61)`

None side is equal. So it's not an isosceles triangle.

2). For a point (3, 1),

Distance between (3, 1) and (-2, -4) =
`√((3+2)^2+(1+4)^2)=5√(2)`

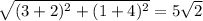
Distance between (3, 1) and (4, -4) =
`√((3-4)^2+(1+4)^2)=√(26)`

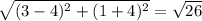
Since none side of the triangle are not equal, triangle is not an isosceles triangle.

3). For (-2,0),

Distance between (-2, 0) and (-2, -4) = 4

Distance between (-2, 0) and (4, -4) =
`√((-2-4)^2+(0+4)^2)` =
`2√(13)`

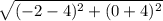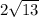
None side is equal so the triangle formed is not an isosceles triangle.

4). For a point (4, 2),

Distance between (4, 2) and (-2, -4) =
`√((4+2)^2+(2+4)^2)=6√(2)`

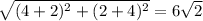
Distance between (4, 2) and (4, -4) =
`√((4-4)^2+(2+4)^2)=6`

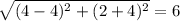
We find the two sides of this triangle measure 6 units therefore, its an isosceles triangle.

Option (4) will be the third point.