Question

Help 15 points!!!!!!!!!!!!!!!!!!!!!

Answer 1

see explanation

Explanation:

Using the tangent ratio in the right triangle

tan A =
`(opposite)/(adjacent)` =
`(BC)/(AC)` =
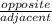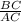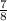`(7)/(8)` , then

∠ A =
`tan^(-1)` (
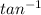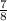`(7)/(8)` ) ≈ 41° ( to the nearest degree )

The sum of the angles in the triangle = 180° , then

∠ B + 41° + 90° = 180°

∠ B + 131° = 180° ( subtract 131° from both sides )

∠ B = 49°

Using Pythagoras' identity in the right triangle

AB² = BC² + AC² = 7² + 8² = 49 + 64 = 113 ( take square root of both sides )

AB =
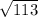`√(113)` ≈ 10.6 ( to the nearest tenth )