We are asked to find the coordinates of point P such that P partitions the directed segment TD in the ratio 5:1. The coordinates of both points are: T (2,1) and D (8,7).
We will use section formula to solve our given problem.
When a point Q divides a segment AB internally in the ratio m:n, then the coordinates of point Q are:
![[\Left x=(mx_2+nx_1)/(m+n),y=(my_2+ny_1)/(m+n)] \right](https://img.qammunity.org/2021/formulas/mathematics/high-school/hwwk83dp7mhqh6nvlzdmu2nob34rv92x35.png)
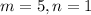 ,
,
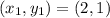 and
and
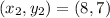 .
.
Upon substituting our given information in above formula, we will get:
![[\Left x=(5(8)+1(2))/(5+1),y=(5(7)+1(1))/(5+1)] \right](https://img.qammunity.org/2021/formulas/mathematics/high-school/uwr9szxr0qrriupl1ysitumr7ta3v120rz.png)
![[\Left x=(40+2)/(6),y=(35+1)/(6)] \right](https://img.qammunity.org/2021/formulas/mathematics/high-school/qq8ifgtuh7mfdv62okn8378pk3wpzyg8b8.png)
![[\Left x=(42)/(6),y=(36)/(6)] \right](https://img.qammunity.org/2021/formulas/mathematics/high-school/7o1ztmsqoyqxnfuse66zt83x3spjdfgoga.png)
![[\Left x=7,y=6] \right](https://img.qammunity.org/2021/formulas/mathematics/high-school/ix8bseh61cbp34g4wl43eerbc60g4glvm5.png)
Therefore, the coordinates of point P are (7,6).