Question

Lori runs 3 miles in 30 minutes. Alexis runs 2 kilometers in 15 minutes. How fast was eachrunner running in miles per hour? Who ran the fastest?

Answer 1

We have been given that Lori runs 3 miles in 30 minutes.

First of all, we will find rate at which Lori runs per minute as:

`\text{Speed}=\frac{\text{Distance}}{\text{Time}}`

`\text{Lori's speed}=\frac{\text{3 miles}}{\text{30 min}}`

`\text{Lori's speed}=\frac{\text{0.1 miles}}{\text{ min}}`

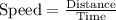
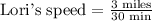
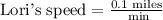
We know that 1 minute equal 60 minutes. Let us convert speed into miles per hour as:

`\text{Lori's speed}=\frac{\text{0.1 miles}}{\text{ min}}* \frac{\text{60 min}}{\text{1 hour}}`

`\text{Lori's speed}=\frac{\text{6 miles}}{\text{hour}}`

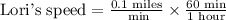
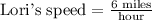
Therefore, Lori runs 6 miles per hour.

We have been given that Alexis runs 2 kilometers in 15 minutes.

We will find rate at which Alexis runs per minute as:

`\text{Alexis's speed}=\frac{\text{2 km}}{\text{15 min}}`

`\text{Alexis's speed}=\frac{\text{2 km}}{\text{15 min}}* \frac{\text{60 min}}{\text{1 hour}}`

`\text{Alexis's speed}=\frac{\text{2 km}}{1}* \frac{4}{\text{1 hour}}`

`\text{Alexis's speed}=\frac{\text{8 km}}{\text{1 hour}}`

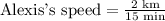
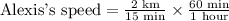
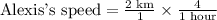
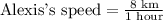
1 km = 0.621371 miles.

8 km =
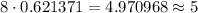`8\cdot 0.621371=4.970968\approx 5` miles.

Therefore, Alexis runs 5 miles per hour.

Since Lori' speed is greater than Alexis's, therefore, Lori ran the fastest.