Question

The shorter leg of a right triangle has a measure of x + 5. The longer leg is one less than three times the length of the shorter leg. The hypotenuse is thirteen more than two times the shorter leg. The area of the triangle, A, is 2.5 times the magnitude of the perimeter.

Create a system of equations to model the situation above. Determine if there are any solutions, and, if possible, whether or not they are viable.

How many total possible solutions of the form (x, A) are there for this situation?

How many total viable solutions of the form (x, A) are there for this situation?

Answer 1

Given:

• 
  `\textsf{Shorter leg}=(x+5)`
• 
  `\textsf{Longer leg}=3(x+5)-1`
• 
  `\textsf{Hypotenuse}=2(x+5)+13`
• 
  `\sf A=2.5P\quad \textsf{(where A is area and P is perimeter)}`

`\begin{aligned} \textsf{Perimeter} & =\textsf{shorter leg + longer leg + hypotenuse}\\ & = (x+5)+[3(x+5)-1]+[2(x+5)+13]\\ & = x+5+3x+15-1+2x+10+13\\ & = 6x+42\end{aligned}`

`\begin{aligned} \textsf{Area} & =\frac12\textsf{(shorter leg)(longer leg)}\\ & =\frac12(x+5)[3(x+5)-1]}\\ & =\frac12(x+5)(3x+14)\\ & = \frac12(3x^2+29x+70)\\ & = \frac32x^2+(29)/(2)x+35 \end{aligned}`

`\begin{aligned} \textsf{Area} & =2.5 \sf (Perimeter)\\ \implies \frac32x^2+(29)/(2)x+35 & =\frac52(6x+42)\\ 3x^2+29x+70 & =5(6x+42)\\ 3x^2+29x+70 & =30x+210\\ 3x^2 -x-140 & =0\\ 3x^2-21x+20x-140 & =0\\ 3x(x-7)+20(x-7) &=0\\ (x-7)(3x+20)& =0\end{aligned}`

Therefore:

`(x-7)=0 \implies x=7`

`(3x+20)=0 \implies x=-(20)/(3)`

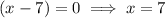
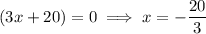
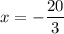`x=-(20)/(3)` is not a viable solution as when inputting this into the formula for the shorter leg, it gives a negative value:

`\textsf{Shorter leg}=-(20)/(3)+5=-\frac53`

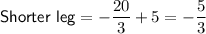
As distance cannot be negative, this is not a viable solution.

When x = 7:

`\textsf{Shorter leg}=7+5=12`

`\textsf{Longer leg}=3(7+5)-1=35`

`\textsf{Hypotenuse}=2(x+5)+13=37`

`\textsf{Perimeter}=6(7)+42=84`

`\textsf{Area} & =\frac32(7)^2+(29)/(2)(7)+35=210`

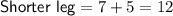
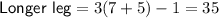
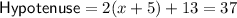
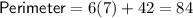
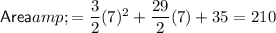
Therefore, there is one viable solution. This solution in the form (x, A) is (7, 210)