Question

Rubi tosses a quarter off the Main Street bridge into the St. John’s River. The distance, in feet, the quarter is above the water is modeled by the equation d(t) = −16t2+96t + 112, where t represents time in seconds.

Find the actual value(s) now to each question. Use the solution from the previous question to assist you with what you are actual solving for.

(a) From what height was the quarter tossed?

The quarter was tossed at 112 feet.

(b) How long does it take the quarter to reach its maximum height?

It will take ________ seconds for the quarter to reach its maximum height.

(c) What is the maximum height of the quarter?

The maximum height of the quarter is ________ feet.

(d) How much time does it take for the quarter to hit the water?

It will take ______ seconds for the quarter to hit the water.

Answer 1

The given function is

`d(t)=-16t^(2)+96t+112`

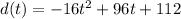
This function models the distance the quarter is above the water.

In this case, the x-axis represents the water level.

(a)

The coin was tossed at 112 feet, because that's the initial valur of the given function. Notice that the constant term is 112, which doesn't depend on any variable, that means it's a number that won't change, because that's the initial height.

(b)

To find the maximum height, we need to find the vertex of the function, which has coordinates of
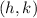`(h,k)`, where
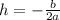`h=-(b)/(2a)` and
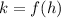`k=f(h)`. Also, from the equation we know
`a=-16`,
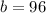`b=96` and
`c=112`.

Using these values, we can find the vertex

`h=-(96)/(2(-16))=(96)/(32)=3`

`k=f(3)=-16(3)^(2) +96(3)+112=-144+288+112=256`

The maximum height is 256 feet, and the time needed to reach it was 3 seconds.

(c)

As we found before, the maximum height is 256 feet.

(d)

After 6 seconds the quarter will hit the water. This answer is found by deduction only, because, if the maximum height took 3 seconds, then it would take 3 seconds more to hit the water.