Answer:
k = 0, k = 4
Explanation:
Given equation:
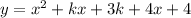
Rearrange into standard form
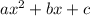 :
:
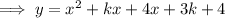
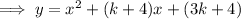
Therefore:
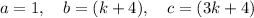
If the vertex lies in the x-axis, then the quadratic has one (repeating) root at (x, 0). Therefore, we can use the discriminant to find the values of k.
Discriminant
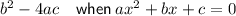
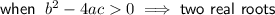
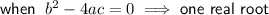
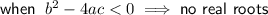
Therefore, set the discriminant to zero and solve for k:
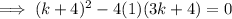
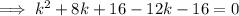
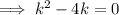
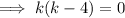
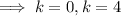
So the vertex lies in the x-axis when k = 0 or k = 4