Solve this 4\left(5x-2\right)=2\left(9x+3\right)

Question

Solve this

`4\left(5x-2\right)=2\left(9x+3\right)`

Answer 1

• 7

`\:`

Explanation:

In the above question, we have to solve the equation and find the value of x. So,

`\\ {\longrightarrow \pmb{\sf {\qquad 4(5x-2)=2(9x+3) }}} \\ \\`

Using distributive property we get :

`\\ {\longrightarrow \pmb{\sf {\qquad 20x-8=18x+6 }}} \\ \\`

Adding (-18x) to both sides we get :

`\\ {\longrightarrow \pmb{\sf {\qquad 20x-8 + ( - 18x)= \cancel{18x}+6 + \cancel{( - 18x) }}}} \\ \\`

`{\longrightarrow \pmb{\sf {\qquad 2x-8=6 }}} \\ \\`

Now Adding 8 to both sides we get :

`\\ {\longrightarrow \pmb{\sf {\qquad 2x-8 + 8=6 + 8 }}} \\ \\`

`{\longrightarrow \pmb{\sf {\qquad 2x=14 }}} \\ \\`

Dividing both sides by 2 we get :

`\\ {\longrightarrow \pmb{\sf {\qquad (2x)/(2) = (14)/(2) }}} \\ \\`

`{\longrightarrow \pmb{\frak {\qquad x=7 }}} \\ \\`

Therefore,

• The value of x is 7

Answer 2

• Solution of equation ( x ) = 7

Explanation:

In this question we have given with an equation that is 4 ( 5x - 2 ) = 2 ( 9x + 3 ). And we are asked to solve this equation that means we have to find the value of x.

Solution : -

`\quad \longrightarrow \: 4 ( 5x - 2 ) = 2 ( 9x + 3 )`

Step 1 : Removing parenthesis :

`\quad \longrightarrow \:20x - 8 = 18x + 6`

Step 2 : Adding 8 from both sides :

`\quad \longrightarrow \:20x - \cancel{ 8 }+ \cancel{8} = 18x + 6 + 8`

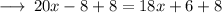
On further calculations we get :

`\quad \longrightarrow \:20x = 18x + 14`

Step 3 : Subtracting 18 from both sides :

`\quad \longrightarrow \:20x - 18x = \cancel{18x }+ 14 - \cancel{18}`

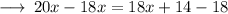
On further calculations we get :

`\quad \longrightarrow \:2x = 14`

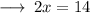
Step 4 : Dividing with 2 on both sides :

`\quad \longrightarrow \: \frac{ \cancel{ 2}x}{ \cancel{2}} = \cancel{(14)/(2) }`

On further calculations we get :

`\quad \longrightarrow \: \blue{\boxed{ \frak{x = 7}}}`

• Therefore, solution of this equation is 7 or we can say that value of this equation is 7 .

Verifying : -

We are verifying our answer by substituting value of x in given equation. So ,

• 4 ( 5x - 2 ) = 2 ( 9x + 3 )

• 4 [ 5 ( 7 ) - 2 ] = 2 [ 9 ( 7 ) + 3 ]

• 4 ( 35 - 2 ) = 2 ( 63 + 3 )

• 4 ( 33 ) = 2 ( 66 )

• 132 = 132

• L.H.S = R.H.S

• Hence, Verified.

Therefore, our value for x is correct .

#Keep Learning