Question

Given the function g(x)=x^2+2x-5g(x)=x

2
+2x−5, determine the average rate of change of the function over the interval -6\le x \le 1−6≤x≤1.

Answer 1

We have been given a function
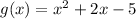`g(x)=x^2+2x-5`. We are asked to find average rate of change of the function over the interval
`-6\leq x\leq 1`.

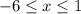We will use average rate of change formula to solve our given problem.

`\text{Average rate of change}=(f(b)-f(a))/(b-a)`

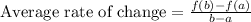
For our given function
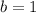`b=1` and
`a=-6`.

`\text{Average rate of change}=(g(1)-g(-6))/(1-(-6))`

`g(1)=1^2+2(1)-5`

`g(1)=1+2-5`

`g(1)=-2`

`g(-6)=(-6)^2+2(-6)-5`

`g(-6)=36-12-5`

`g(-6)=19`

`\text{Average rate of change}=(-2-19)/(1+6)`

`\text{Average rate of change}=(-21)/(7)`

`\text{Average rate of change}=-3`

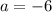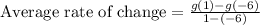
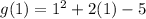
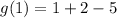
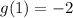
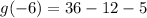
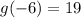
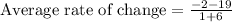
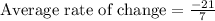
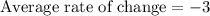
Therefore, the average rate of change of the function is
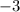`-3` over the interval
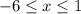`-6\leq x\leq 1`.