Answer:
The description for the problem is listed throughout the section below on explanations.
Explanation:
The given values are:
The amount of bank loan = $22,000
Interest rate = 7.99%
Pays monthly = $700
So, the principal amount decreases by 700 per month.
Now,
The principal amount at the end of the
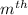 month = (22000 - 700 m)
month = (22000 - 700 m)
Then,
The interest paid at the end of 1 year:
⇒
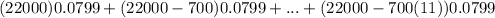
On simplifying the above equation, we get
⇒
![0.0799[12(22000)-(11* 12)/(2)* 700]](https://img.qammunity.org/2021/formulas/mathematics/college/mmv9qykzmdvvw1tng1r9dwagkhu1a5uoh1.png)
⇒
![0.0799[264000-11* 6* 700]](https://img.qammunity.org/2021/formulas/mathematics/college/wjimoptxmnpgme2r11gjrz2zr1sd8jld9g.png)
⇒
![0.0799[264000-46200]](https://img.qammunity.org/2021/formulas/mathematics/college/wwh2mubhjew14t704jgm1fj9obyhyubrz4.png)
⇒ $
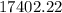
Therefore interest could be measured correctly at the end of each year, likewise.
⇒
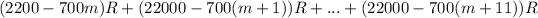
⇒
![R[12* 22000-700[12m+(11* 12)/(2)]]](https://img.qammunity.org/2021/formulas/mathematics/college/r9nlxaufo6vijv8lp3y9rs3q0mhenmdxhi.png)
⇒
![R[264000-700[12m+(11* 12)/(2)]]](https://img.qammunity.org/2021/formulas/mathematics/college/32uo8399qdk8pa99m1p2u0ro5z8zqedodt.png)
⇒
![R[263300(12m+66)]](https://img.qammunity.org/2021/formulas/mathematics/college/zmzg8fnwxqs2ecqn9awzudwv9z08gas8de.png)
R : interest rate