Question

High-power experimental engines are being developed by the Stevens Motor Company for use in its new sports coupe. The engineers have calculated the maximum horsepower for the engine to be 580HP. Sixteen engines are randomly selected for horsepower testing. The sample has an average maximum HP of 610 with a standard deviation of 55HP. Assume the population is normally distributed. Step 2 of 2 : Use the confidence interval approach to determine whether the data suggest that the average maximum HP for the experimental engine is significantly different from the maximum horsepower calculated by the engineers.

Answer 1

The calculated value t = 2.18 > 1.753 at 5% level of significance.

we accepted the Alternative hypothesis

Hence the data suggest that the average maximum HP for the experimental engine is significantly different from the maximum horsepower calculated by the engineers.

Explanation:

Step(i):-

Given sample size 'n' =16

Given data the engineers have calculated the maximum horsepower for the engine to be 580HP

Mean of the Population 'μ' = 580HP

Mean of the sample size 'x⁻' =610

The sample standard deviation 'S' = 55HP

Null hypothesis: H₀:There is no significant difference between the average maximum HP for the experimental engine and maximum horsepower calculated by the engineers.

That is H₀: x⁻ = μ

Alternative hypothesis: H₁: x⁻ ≠ μ

Step(ii):-

The test statistic

`t = (x^(-) -mean)/((S)/(√(n) ) )`

`t = (610 -580)/((55)/(√(16) ) )`

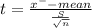
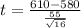
t = 2.18

The degrees of freedom ν=n-1 =16-1=15

The tabulated value

t₀.₉₅ = 1.753

The calculated value t= 2.18 > 1.753 at 95% of level of significance

The null hypothesis is rejected

we accepted the Alternative hypothesis

Conclusion:-

Hence the data suggest that the average maximum HP for the experimental engine is significantly different from the maximum horsepower calculated by the engineers.