Answer:
(-4,9) and (7,5)
Explanation:
The line QR belongs to the following family of line segments:
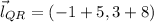

The length of the line segment is:
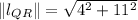
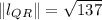
A segment is congruent to that family of segments only if its family of line segments has the same length. Then:
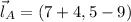
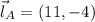
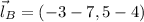
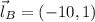


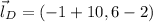

Only the first option satisfies the condition of congruence, whose length is:

