Question

41. Two antenna towers, 400 m apart, are to be supported by a single cable anchored at a common point between them. One tower is 20 m high, and the other tower is 60 m high. At what point should the anchor be located to use a minimum amount of cable? Geometry

Answer 1

The anchor should be located at the midpoint between the 20m high and 60m high antennas.

Explanation:

Let the length of cable for 20m high antenna be represented by x, and that for 60m high antenna be y.

The single length of cable required = x + y.

From the principle of geometry, if the cable is anchored at 200m from the 20m high antenna, it forms a right angled triangle. Applying the Pythagoras theorem,

x =
`\sqrt{200^(2) - 20^(2) }`

= 199

Applying the same principle to the 60m high antenna gives,

y =
`\sqrt{200^(2) - 60^(2) }`

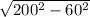
= 191

The single length of cable required = 199+ 191

= 390m

Varying the point of location of the anchor between the two antennas causes an increase in the length of cable required.

The anchor should be located at the midpoint between the two antennas to achieve a minimum amount of cable.