Question

When engaging in weight-control (fitness/fat burning) types of exercise, a person is expected to attain about 60% of their maximum heart rate. For 20-year-olds, this rate is approximately 120 bpm. A simple random sample of one hundred 20-year-olds was taken, and the sample mean was found to be 107 bpm with a standard deviation of 45 bpm. Researchers wonder if this is evidence to conclude that the expected level is actually lower than 120 bpm.

a. What is the (sample estimate for the) standard error of the mean?
b. We are interested in a 95% confidence interval for the 20-year-old population mean bpm (when engaging in weight control types of exercise). What is the margin of error associated with the confidence interval?
c. What is the 95% confidence interval for the 20-year-old population mean bpm based on this data?
d. What is the interpretation of the 95% confidence interval you computed in part C?

Answer 1

a) standard error of the mean =10.06

b) The margin of error = 17.3982

c) 95% of confidence intervals are

`(89.6018 ,124.3982)`

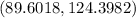
d) Lower limit of 95% of confidence interval = 89.6018

upper limit of 95% of confidence interval = 124.3982

The Population mean is lies between in these intervals

Explanation:

Step(i):-

Given sample size 'n' = 20

Given sample mean was found to be 107 bpm with a standard deviation of 45 bpm.

Sample mean
`x^(-) = 107 bpm`

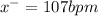
Sample standard deviation (S) = 45 bpm

a) standard error of the mean is determined by

`S.E = (S)/(√(n) ) = (45)/(√(20) )`

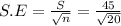
S.E = 10.06

b) The margin of error is determined by

`M.E = (t_(\alpha ) X S )/(√(n) )`

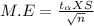
The degrees of freedom ν
`= n-1 =20-1=19`

`t_(\alpha ) = 1.729`

`M.E = (1.729X 45)/(√(20) )`

`M.E = (77.805 )/(4.472 ) = 17.3982`

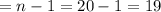
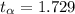
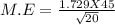
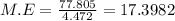
c) 95% of confidence intervals are determined by

`(x^(-) - t_(\alpha ) (S)/(√(n) ) , x^(-) + t_(\alpha ) (S)/(√(n) ) )`

`(107 - 1.729(45)/(√(20) ) , 107 + 1.729(45)/(√(20) ) )`

`(107 - 17.3982 } , 107 +17.3982 )`

`(89.6018 ,124.3982)`

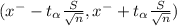
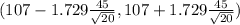
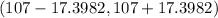
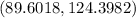
d)

Lower limit of 95% of confidence interval = 89.6018

upper limit of 95% of confidence interval = 124.3982

The Population mean is lies between in these intervals