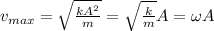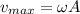a)E= U + K =
 kx² +
kx² +
 mv²
mv²
The total energy of the system at any point in the motion is equal to the sum of the elastic potential energy of the spring, U, and of the kinetic energy of the mass, K:
E= U + K =
 kx² +
kx² +
 mv²
mv²
where
'k' represents the spring constant
'x' is the compression/stretching of the spring with respect to its equilibrium position
'm' is the mass of the block attached to the spring
and 'v' is the speed of the block
b) A=

The amplitude of the motion compares to the most extreme displacement of the mass-spring system. The displacement of the system, x(t), at time t, for a simple harmonic oscillator is given by,
x= Asin(ωt+∅)
where
amplitude is 'A'
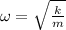 is the angular frequency of the motion
is the angular frequency of the motion
t is the time
 is the phase (we can take
is the phase (we can take
 =0 )
=0 )
The amplitude of the motion occurs when the displacement of the motion is maximum: x=A. Regarding energy, the mass-spring system is at its maximum displacement (x=A) when all the mechanical energy of the framework is elastic potential energy, so when the kinetic energy is zero:
K=
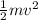 =0
=0
E=
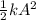 -->(1)
-->(1)
A=

c)
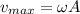
When the elastic potential energy is zero, the maximum speed of the system occurs i.e U=0 and the kinetic energy is maximum, so:
U=0
E=

According to the law of conservation of the mechanical energy, this energy must be equal to the energy of the system at its maximum displacement (1), so we can write
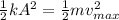
and solving for
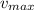 we find an expression for the maximum speed:
we find an expression for the maximum speed: