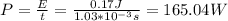Question

A carbon dioxide laser used in surgery emits infrared radiation with a wavelength of 10.6 µm. In 1.03 ms, this laser raised the temperature of 0.101 mm3 of flesh to 100°C and evaporated it. (Assume that the initial temperature of the flesh is 37.0°C, the heat of vaporization of water is 2,256 kJ/kg, the specific heat of flesh is the same as that of water, 4,186 J/(kg · °C), and the density of flesh is the same as that of water, 1,000 kg/m3.)

a. How many photons were required?
b. What was the minimum power output during the flash?

Answer 1

a) 9*10^18 photons

b) 165.04 W

Step-by-step explanation:

a. To find the number of photons you first calculate the energy used to rise the temperature of the flesh ans the energy necessary to evaporate the water. All this contribution is given by the following formula:

`Q=Q_T+Q_E`

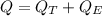
QT: energy to rise the temperature

QE: energy to evaporate the water

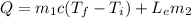`Q=m_1c(T_f-T_i)+L_e m_2` ( 1 )

m1: mass of the flesh

m2: mass of the water

Le: heat of vaporization of water

You take into account that approximately 75% of the substance in flesh is water. Hence, the mass of water will be:

`m_2=0.75\rho V=0.75(1000kg/m^3)(0.101(10^(-3)m)^3)=7.57*10^(-8)kg`

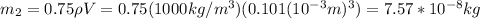
And the mass of flesh:

`m_1=0.25(1000kg/m^3)(0.101(10^-3m)^3)=2.52*10^(-8)kg`

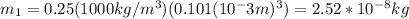
you replace the values of the parameters in the equation (1) to obtain:

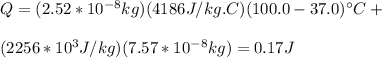`Q=(2.52*10^(-8)kg)(4186J/kg.C)(100.0-37.0)\°C+\\\\(2256*10^3 J/kg)(7.57*10^(-8)kg)= 0.17J`(2)

0.17 J is the energy required

Next, you calculate the energy of a 10.6µm photon:

`E_p=h\\u=h(c)/(\lambda)\\\\h=6.62*10^(-34)Js\\\\c=3*10^8m/s\\\\\lambda=10.6*10^(-6)m\\\\E_p=(6.62*10^(-34)Js)((3*10^8m/s)/(10.6*10^(-6)m))=1.87*10^(-20)J`

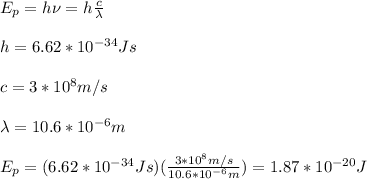
you divide the energy obtained in (2) with Ep to get the number of photons:

`n_p=(0.17J)/(1.87*10^(-20))\approx9*10^(18)\ photons`

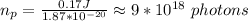
b. To find the minium power output you use:

`P=(E)/(t)=(0.17J)/(1.03*10^(-3)s)=165.04W`