Question

Question

A manufacturer is interested in the output voltage of a power supply used in a PC. Output voltage is assumed to be normally distributed, with standard deviation 0.25 Volts, and the manufacturer wishes to test H0: μ = 5 Volts against H1: μ ≠ 5 Volts, using n = 8 units. If the sample mean is x¯¯=4.85 what can you say about the population mean with a=0.05 significance level ?

Answer 1

The population mean is 5 volts

Explanation:

Output voltage is assumed to be normally distributed, with standard deviation 0.25 Volts

s=0.25

n = 8

`H_0:\mu = 5\\H_a:\mu \\eq 5`

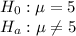
Sample mean =
`\bar{x}=4.85`

Since n < 30 and population standard deviation is unknown

So, we will use t test

Formula :
`t = (x-\mu)/((s)/(√(n)))`

`t = (4.85-5)/((0.25)/(√(8)))`

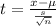
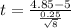
t=-1.69

Refer the t table for p value

Degree of freedom = n-1 = 8-1 = 7

So,
`t_((df,\alpha))=t_(7,0.05)=2.365`

P value >α

So, We are failed to reject null hypothesis

Hence The population mean is 5 volts