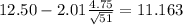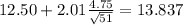Answer:
a) Null hypothesis:
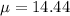
Alternative hypothesis:
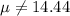
b)
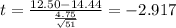
The degrees of freedom are given by:
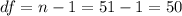
Now we can calculate the p value taking in count the alternative hypothesis
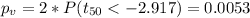
Since the p value is lower than the significance
 we have enough evidence to reject the null hypothesis and the true mean is significantly different from 14.44
we have enough evidence to reject the null hypothesis and the true mean is significantly different from 14.44
c)
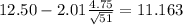
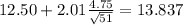
Explanation:
Information given
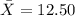 represent the mean for the daily iron intake
represent the mean for the daily iron intake
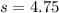 represent the sample deviation
represent the sample deviation
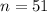 sample size
sample size
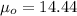 represent the reference value
represent the reference value
 represent the significance level for the hypothesis test.
represent the significance level for the hypothesis test.
t would represent the statistic
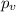 represent the p value for the test
represent the p value for the test
Part a
We want to test if the mean iron intake among the low-income group is different from that of the general population, the system of hypothesis would be:
Null hypothesis:
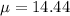
Alternative hypothesis:
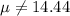
Part b
Since we don't know the population deviation the statistic would be given by:
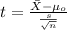 (1)
(1)
Replacing the info we got
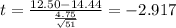
The degrees of freedom are given by:
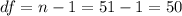
Now we can calculate the p value taking in count the alternative hypothesis
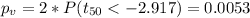
Since the p value is lower than the significance
 we have enough evidence to reject the null hypothesis and the true mean is significantly different from 14.44
we have enough evidence to reject the null hypothesis and the true mean is significantly different from 14.44
Part c
The confidence interval would be given by:
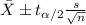
For the 95% confidence interval we can find the critical value in a t distribution with 50 degrees of freedom and we got:
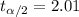
And replacing we got: