Question

A sample of 16 cookies is taken to test the claim that each cookie contains at least 9 chocolate chips. The average number of chocolate chips per cookie in the sample was 7.875. The standard deviation of the population is 2. Assume the distribution of the population is normal. Let μ denote the average number of chocolate chips in all the cookies. The hypothesis to test the claim is: H0 : μ ≥ 9 H1 : μ < 9.

a) what is the test statistic
b) the critical value for this test at a 0.5 level of significance is
c) the p-value for this test statistic is
d) at a 0.5 level of significance, it can be concluded that the mean of the population is

Answer 1

(a) The value of z test statistics is -2.25.

(b) At 0.05 significance level the z table gives critical value of -1.645 for left-tailed test.

(c) The p-value for this test statistic is 0.0122.

(d) We conclude that the average number of chocolate chips in all the cookies is less than 9.

Explanation:

We are given that a sample of 16 cookies is taken to test the claim that each cookie contains at least 9 chocolate chips.

The average number of chocolate chips per cookie in the sample was 7.875. The standard deviation of the population is 2.

Let
`\mu` = the average number of chocolate chips in all the cookies.

So, Null Hypothesis,
`H_0` :
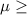`\mu \geq` 9 {means that the average number of chocolate chips in all the cookies is at least 9}

Alternate Hypothesis,
`H_A` :
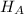`\mu` < 9 {means that the average number of chocolate chips in all the cookies is less than 9}

The test statistics that would be used here One-sample z test statistics as we know about the population standard deviation;

T.S. =
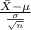`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample mean number of chocolate chips per cookie = 7.875

`\sigma` = population standard deviation = 2

n = sample of cookies taken = 16

So, the test statistics =
`(7.875-9)/((2)/(√(16) ) )`

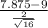
= -2.25

(a) The value of z test statistics is -2.25.

(b) Now, at 0.05 significance level the z table gives critical value of -1.645 for left-tailed test.

Since our test statistic is less than the critical value of z as -2.25 < -1.645, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

(c) The P-value of the test statistics is given by;

P-value = P(Z < -2.25) = 1 - P(Z
`\leq` 2.25)

= 1 - 0.9878 = 0.0122

(d) Therefore, we conclude that the average number of chocolate chips in all the cookies is less than 9.