Question

In the past decades there have been intensive antismoking campaigns sponsored by both federal and private agencies. In one study of national smoking trends, two random samples of U.S. adults were selected in different years: The first sample, taken in 1995, involved 4276 adults, of which 1642 were smokers. The second sample, taken in 2010, involved 3908 adults, of which 1415 were smokers. The samples are to be compared to determine whether the proportion of U.S. adults that smoke declined during the 15-year period between the samples.

Let p1 be the proportion of all U.S. adults that smoked in 1995. Let p2 denote the proportion of all U.S. adults that smoked in 2010.
Reference: Ref 21-4
The P-value of the test for equality of the proportion of smokers in 1995 and 2010 is:_________.
A. greater than 0.10.
B. between 0.05 and 0.10.
C. between 0.01 and 0.05.
D. below 0.01.

Answer 1

`z=\frac{0.384-0.362}{\sqrt{0.374(1-0.374)((1)/(4276)+(1)/(3908))}}=2.055`

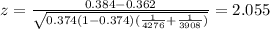
The p value can be calculated from the alternative hypothesis with this probability:

`p_v =2*P(Z>2.055)=0.0399`

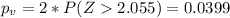
And the best option for this case would be:

C. between 0.01 and 0.05.

Explanation:

Information provided

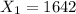`X_(1)=1642` represent the number of smokers from the sample in 1995

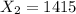`X_(2)=1415` represent the number of smokers from the sample in 2010

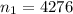`n_(1)=4276` sample from 1995

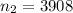`n_(2)=3908` sample from 2010

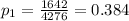`p_(1)=(1642)/(4276)=0.384` represent the proportion of smokers from the sample in 1995

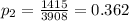`p_(2)=(1415)/(3908)=0.362` represent the proportion of smokers from the sample in 2010

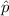`\hat p` represent the pooled estimate of p

z would represent the statistic

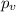`p_v` represent the value for the pvalue

System of hypothesis

We want to test the equality of the proportion of smokers and the system of hypothesis are:

Null hypothesis:
`p_(1) = p_(2)`

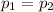
Alternative hypothesis:
`p_(1) \\eq p_(2)`

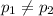
The statistic is given by:

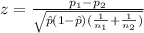`z=\frac{p_(1)-p_(2)}{\sqrt{\hat p (1-\hat p)((1)/(n_(1))+(1)/(n_(2)))}}` (1)

Where
`\hat p=(X_(1)+X_(2))/(n_(1)+n_(2))=(1642+1415)/(4276+3908)=0.374`

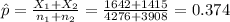
Replacing the info given we got:

`z=\frac{0.384-0.362}{\sqrt{0.374(1-0.374)((1)/(4276)+(1)/(3908))}}=2.055`

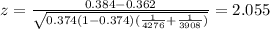
The p value can be calculated from the alternative hypothesis with this probability:

`p_v =2*P(Z>2.055)=0.0399`

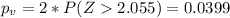
And the best option for this case would be:

C. between 0.01 and 0.05.