Question

The string of a flying kite is being held five feet off the ground. It makes a 60 degree angle with one side parallel to the ground. If all 300 feet of string are out, and there is no sag in the string, how high is the kite above the ground? Billy says using cosine he got a height of 150' + 5' (off the ground) for a total of 155', but Maria argues that using special right triangles the height is approximately 260' + 5' for a total of 265'. Who is right and why?

Answer 1

Maria is right

Height=265 ft

Explanation:

In the attached diagram, the length of the kite is BC and the height of the Kite above the ground is CE.

Now, CE=CD+DE

DE=5 ft

Next, we have to determine the length of CD.

In Triangle BCD

`sin\:60^\circ=(|CD|)/(300) \\|CD|=300*sin 60\\|CD|\approx260\:ft`

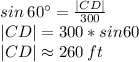
Therefore:

CE=260+5=265 ft

From the above, we see that Maria is right.

Billy erroneously applied the wrong trigonometric ratio (Cosine) which made him get a value of 150ft.