Question

Most geologists believe that the dinosaurs became extinct 65 million years ago when a large comet or asteroid struck the earth, throwing up so much dust that the sun was blocked out for a period of many months. Suppose an asteroid with a diameter of 5.0 km and a mass of 2.5*10^14 kg hits the earth with an impact speed of 4.0*10^4 m/s.

Part A: What is the earth's recoil speed after such a collision? Assume that the mass of the earth is 5.98*10^24 kg. (Use a reference frame in which the earth was initially at rest.)

Part B: What percentage is this of the earth's speed around the sun? Assume that the orbit of the earth is a circle with the radius of 1.5*10^11 m.

Answer 1

1.67 x 10 ⁻⁶ m/s

i think thats your answer

i did the problem an got that so like

I hope I helped :D

Step-by-step explanation:

Answer 2

A) 1.67 x 10 ⁻⁶ m/s

B)5.59 x
`10^-^9` %

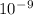Step-by-step explanation:

A)

Given:

d = 5.0 km,

mₐ = 2.5 x
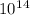`10^1^4` kg

u₁ = 4.0 x 10⁴ m/s

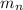`m_n` = 5.98 x 10 ²⁴ kg

Solve using kinetic conserved energy

mₐ x u₁ +
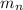`m_n` x u₂ = uₓ x (mₐ +
`m_n` )

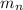(2.5 x
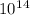`10^1^4`) (4.0 x 10⁴ )+ (5.98 x 10 ²⁴ )(0) = uₓ x (2.5 x
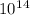`10^1^4` + 5.98 x 10 ²⁴ )

uₓ = ( 2.5 x
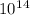`10^1^4` x 4.0 x 10⁴ ) / (2.5 x
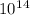`10^1^4` + 5.98 x 10 ²⁴ )

uₓ = 1.67 x 10 ⁻⁶ m/s

B) Assuming earth radius as a R = 1.5 x 10 ¹¹ m

t = 365 days x 24 hr / 1 day x 60 minute / 1 hr x 60s / 1 minute = 31536000 s

t = 31536000 s

D = 2 π R = 2 π( 1.5 x 10 ¹¹ )

D = 9.4247 x 10 ¹¹ m

u₂ = D / t = 9.4247 x 10 ¹¹ / 31536000

u₂ = 29885.775 m/s

% = ( 1.67 x 10 ⁻⁶ m/s ) / (29885.775 m/s) x 100

% = 5.59 x
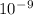`10^-^9` %